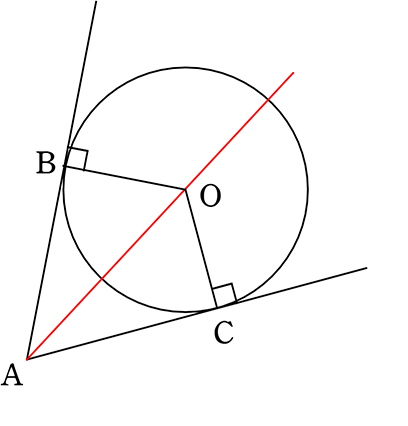
5図形の性質と証明 円の接線を作図しよう 10 2 年 組 氏名 1 古代ギリシアの数学者ユークリッドは,いくつかの基本的な図形の性質をもとにして, 様々な図形の性質を証明し,有名な「原論」にまとめました。 この原論の第3巻に,「与えられた点から与えられた円に接線をひく」作図の方法が紹介3つの円が互いに2点で交わるとき,3本の根軸は一点で交わる。 2つの円が2点で交わるとき,その2点を結んだ線を 根軸 (radical axis)と言います。 3本の根軸が1点で交わるというのはおもしろいです! このページでは,根心の存在定理を3段階に分けて証明します。円の外にある 1 点からその円に引いた 2 本の接線の長さは等しい 。 これは以下のように証明ができます。 下の図のように,円 に円の外側の点 から 2 本の接線を引き,その接点を , とする。 と において, 線分 , は円 の接線なので, ① は共通 ②

円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
円の性質 中学 証明
円の性質 中学 証明- 内接円の性質 内接円には、大きく \(2\) つの性質があります。 性質①内心と各辺の距離 多角形のそれぞれの辺が内接円の接線となっていて、各接点から引いた垂線の交点が内接円の中心(内心)となります。証明 円周角と中心角の関係より ∠ A ∠ C = 1 2 × 36 0 ∘ = 18 0 ∘ \angle A\angle C=\dfrac {1} {2}\times 360^ {\circ}=180^ {\circ} ∠A∠C = 21 × 360∘ = 180∘ (赤+青= 1 2 \dfrac {1} {2} 21




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
「不思議な公式の証明!」 ~性質が成り立つ理由を式を使って説明する~ ☆本時のねらい:展開や因数分解を利用して図形の性質を証明することができる。 ☆本時の工夫点:①証明のかき方に慣れるために,教科書の証明を読み取り,理解する 時間を設定する。 ②面積を求める公式S=al に円の外接円の周上の点 から,直線 , , に 垂線 , , を下ろす。 このとき,垂線の足, , , の 3 点が一直線上に存在 します。 このことをシムソンの定理といいます。証明は以下のようにすることができます。 線分 , をひく。 より, , , , は を直径とする円周上にある。傍接円、傍心について 中学生へ 三角形の外角の二等分線の交点を「傍心ほ(ぼ)うしん」といい、傍心は全部で3つあり、下の図で ABCの傍心は点P、Q、R の3つです。 1990年ごろの中学の教科書にも傍心という用語は出てきませんが、傍接円と接線の長さ
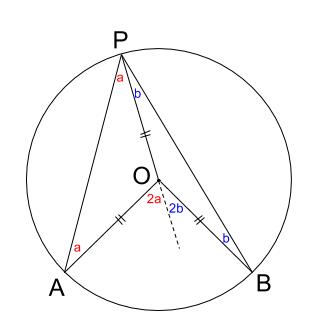
楕円は、円を一定方向に拡大縮小したものであるが、多少形は変わるものの円と同様 の性質が成り立つ。(→参考:「 方べきの定理」) 円 O において、円外の1点 P から円に引いた2つの接線のなす角は、直線 OP により 2等分される。 証明は明らかだろう。 直角三角形OPAと直角三角形OPBが合同「円に潜む性質!」 ひそ ~証明に用いる図形の性質を読み取る~ ☆本時のねらい:円周角の定理の証明において,用いられている図形の性質を読み取る ことができる。 ☆本時の工夫点:①図の中の角度を実測し円周角の定理を予想させることで,証明する ことに目的意識をもたせる。 ②円の性質の考察に関心を持ち,意欲的に取り組むことができる。 円に関する性質を見出し,それを証明したり,定理の相互関係を明らかにしたりす ることができる。 円に関する定理を的確に用いて,図形の問題に対し見通しを持ち,論理的に考察し, 解決することができる。 円に関する用語
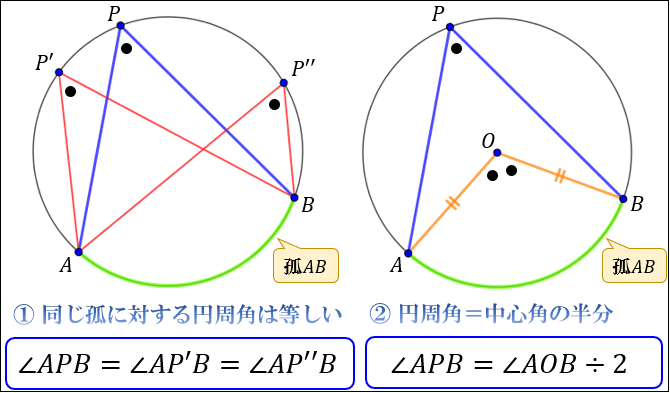
直径pokを引くと,(ア)の証明と同様に 3+4で したがって ∠apb=1∠aob 2 <戻る> (ウ) 直径pokを引くと,(ア)の証明と同様に 6-5で したがって ∠apb=1∠aob 2 <戻る>数学 において、 円 (えん、 英 circle )とは、 平面 (2次元 ユークリッド空間 )上の、定点 O からの距離が等しい 点 の集合でできる 曲線 のことをいう。 ここで現れる定点 O を円の 中心 と呼ぶ。 円には、その中心が1つあり、また1つに限る。円周角 (証明) 四角形ABCDは頂点がすべて円周上にあり、AB=DCである。 対角線ACとBDの交点をEとする。 このとき ABE≡ DCEを証明せよ。 A B C D E 図でA,B,C,Dはすべて円周上の点である。 AB=AD,AC=BCのとき ACD≡ BCEを証明せよ。 A B C D E 図のようにBCを直径とする円Oがある。




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



中学数学 円周角 中心角
中学3年生 数学 円の性質の利用 練習問題プリント 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要領(21年度全面実施)への対応作業を進めておりますが、 現在のところ、数学、理科、英語プリントが未対応ともう一つ,三角形の内接円,外接円の接点の性質を,定理の証明で用いるので,先に証明しておきましょう. 命題 ABCの内接円I,傍接円I B と辺ACとの接点をそれぞれD,Eとする.また,2円I,I B の共通内接線 のうち辺ACでない方の直線と辺BC,ABまたはその延長との交点をそれぞれF,GとするPage 4 ここで,三角形abc の外接円は補助円の役目を果たしているが,角aの二等分線と辺bc の交点をd と するとき,'adc の外接円を補助円と考えて証明を試みてみよう. (e)補助円による証明 証明) 'adc の外接円と辺abとの交点をe とすると, 円周角の性質より, ed dc




中3 中3 円周角の定理 円の性質の利用 中学生 数学のノート Clear



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
まずは解答を見てみましょう。 解答 余弦定理より、 cos A = 36 16 − 25 2 × 6 × 4 = 27 2 × 6 × 4 = 9 16 cos A = 36 16 − 25 2 × 6 × 4 = 27 2 × 6 × 4 = 9 16 三角比の相互関係式より、 sin A = √ 1 − cos 2 A = √ 1 − ( 9 16) 2 = √ 256 − 81 16 = 5 √ 7 16 sin A = √ 1 − cos 2 A = √ 1 − ( 9 16) 2 = √ 256 − 81 16 = 5 √ 7 16 ≫参考記事:三角比の相互関係の公式4つって?円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは,a c = 180 を説明 (証明)します。 円 周 角 : に 対 応 す る 中 心 角 は 円 周 角 : に 対 応 す る 中 心 角 は円分多項式 定義1 n 乗して始めて1 になる数を1 の原始n 乗根(primitive nth root) と呼ぶ. n が素数の場合は1 を除くn 乗根は全て原始n 乗根である.つまり,zp = 1 の解 1,ω,ω2,··,ωp¡1 ω = cos 2π p isin 2π p) から1 を除いたp − 1 個の数がそれにあたる.ω = cos π 4 isin π 4 は原始8 乗根のうちの




数学 中3 56 円周角の定理 基本編 Youtube




円の中心角 弧 弦 Jsciencer
九点円の定理とは 九点円の定理とは,三角形と円に関する非常に美しい定理です.受験等に役立つことはほとんどないと思いますが,この定理の美しさを鑑賞する価値は十分あります.ぜひ,秩序だった様を存分に味わってください. 九点円の定理: $ abc$ について,以下の $9$ つの点単元「円の性質」の小単元「円の性質の利用」(3時間)における数学的活動を取り入れた授業展開案です。 単元 円周角 (啓林館) 2 円の性質の利用 ・1・ 円の性質の利用 全3時間 1/3時 ねらい ・ 条件を満たす場面を求めるために、数学の問題におきかえて、円周角の定理を利用して円の性質 2 目標 (1) 円周角と中心角に関心をもち、それらの関係や性質を見い出したり、その証明にどのような図 形の性質が用いられているのかを考えたりしようとしている。 数学への関心・意欲・ 態度 (2)円周角と中心角の関係や 、 同じ弧に対する円周角の性質を見い出すこと




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
垂心の証明 重心は「つりあい」、外心は「外接円」、内心は「内接円」と比較的扱いやすい題材が豊 富なのと、分かりやすさから多分生き残ったのだろう。 それに対して、垂心とか傍心は応用もままならず、扱いにくい題材がゆえに省略された のではないだろうか。 しかしながら、傍心は・図形の性質を証明 することなどに,円 周角と弧の定理や 直径と円周角の定 理を利用すること ができる。 ・円周角と弧の定理 や直径と円周角の 定理を利用して,円 についてのいろい ろな角の大きさを 求めることができ る。 ・円周角と弧の定理 や直径と円周角の円の極と極線は、双対(そうつい)的な関係にあります。 双対性とは幾何学の重要な概念です。 この双対性について、極と極線を通して探っていきましょう。 円の極と極線が、そのまま三角形の極と極線に結びつき、様々な現象を示します。 極線上の点の極線が不思議な現象を示します。



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理の証明
証明は、「ハンバーガーの3ステップ」! 今回は、 「円の性質を使う証明問題」 をやるよ。 「証明」、ニガテな人が多いよね。 そこで、証明の書き方のポイントを紹介するよ。 基本は、 「ハンバーガーの3ステップ」 だよ。Dを中心に三角形の3つの辺に接する 円を書くことができます。 この円を 内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離が等しい点の集まり(軌跡)」と 証明: 直線 $AB$ 上において,線分 $AB$ を $mn$ に内分する点を $C$ とする.また,求める円の半径を $r$,線分 $AB$ の長さを $k$ とおく. 点 $C$ は線分 $AB$ を $mn$ に内分するので, $$BC=\frac{n}{mn}k$$ である.また,点 $O$ は線分 $AB$ を $m^2n^2$ に外分する点であったから, $$OA=\frac{m^2}{m^2n^2}k$$ である.したがって, $$OB=OA




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
まずは「 四角形ADHF,BEHD,CFHEは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。 四角形CFHEに注目すると、, したがって、円周角の定理の逆を用いて、CHを直径とする円が見えてきます。 他の四角形でも同様の証明ができます。 つぎに垂心の性質2「 」の証明をします。 これは三角関数の 正弦円の性質を証明 の根拠として使 うことができる。 円周角の定理を使っ て、相似の証明をす る。 相似条件を成り立 たせるために、円周 角の定理が活用で きることに気付か せる。 ② ④ ワークシートの 記述内容、グルー プ活動での発言 の様子をもとに 確認する。 9 本 時 ・ 10 と 身近な問題




中3数学 円の性質と証明 練習編 映像授業のtry It トライイット



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典



Studydoctor円周角の定理と中心角 中学3年数学 Studydoctor




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
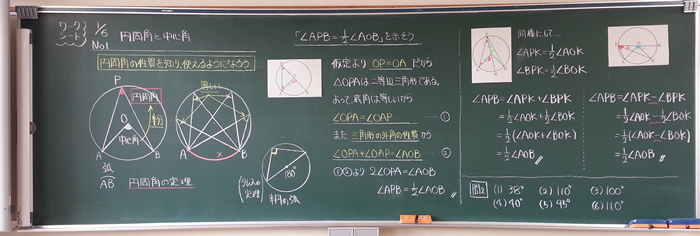



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館




円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
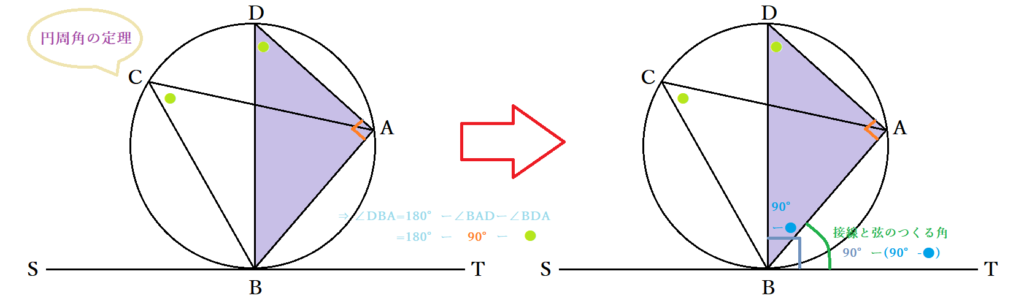



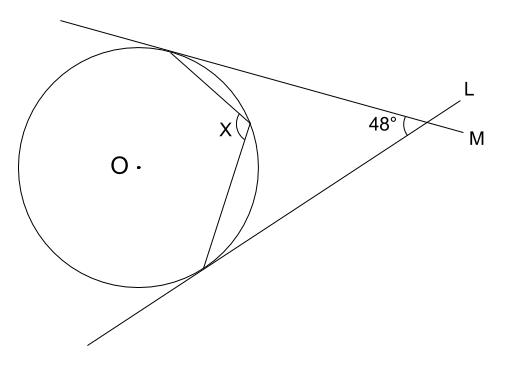
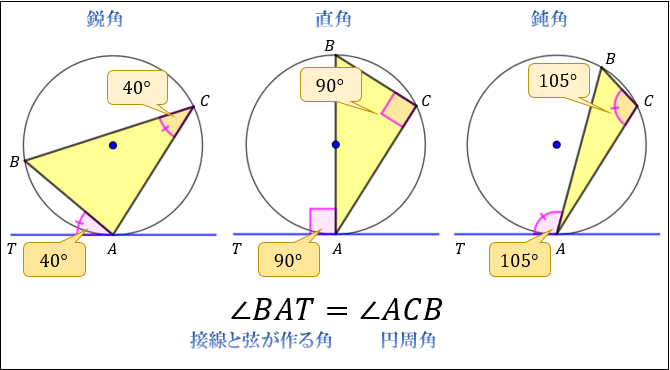
接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog




中3数学 円の性質16 円の性質を利用した証明 Youtube




世界一わかりやすい数学問題集中3 6章 円の性質
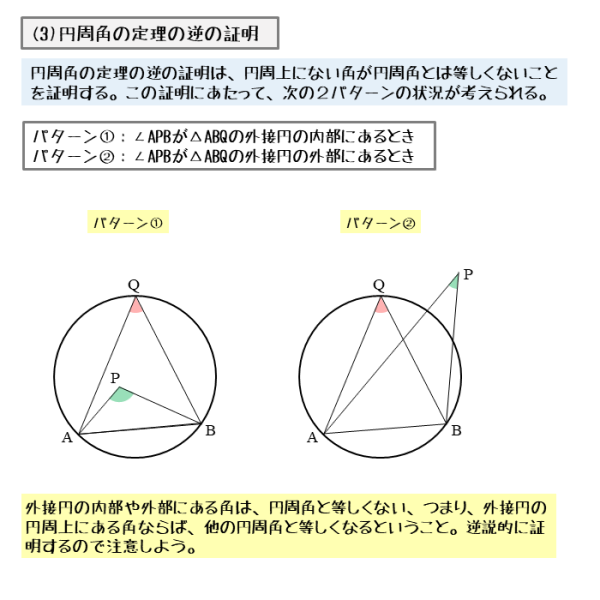



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
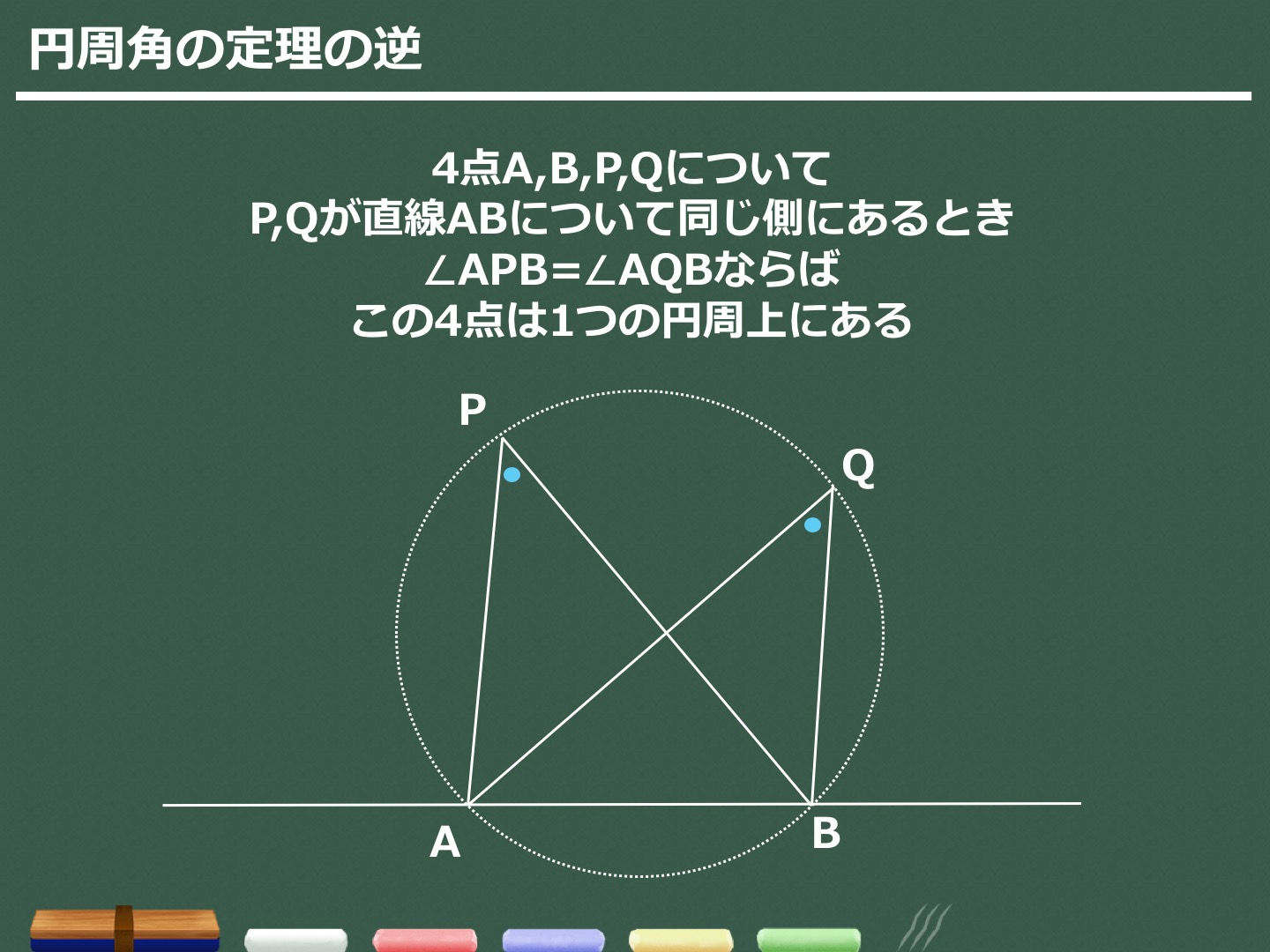



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ



1
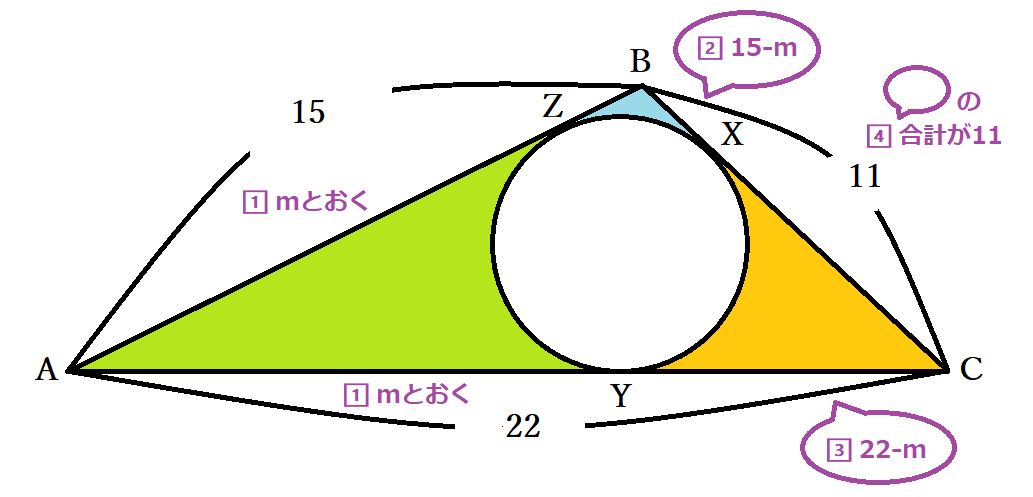



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog
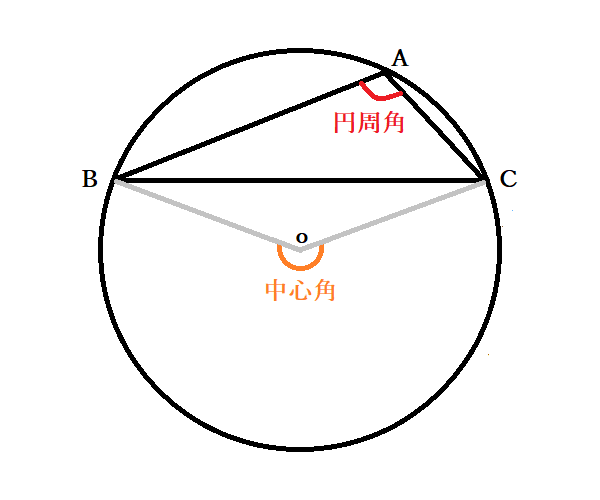



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
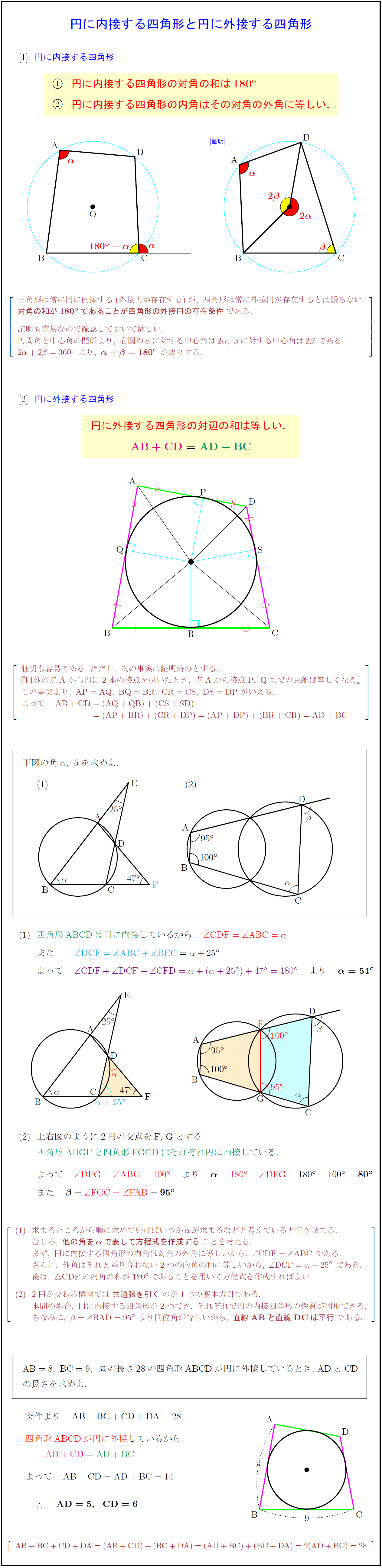



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月




接弦定理の証明 円周角が鈍角ver 数学a By となりがトトロ マナペディア



円周角の定理の証明




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座
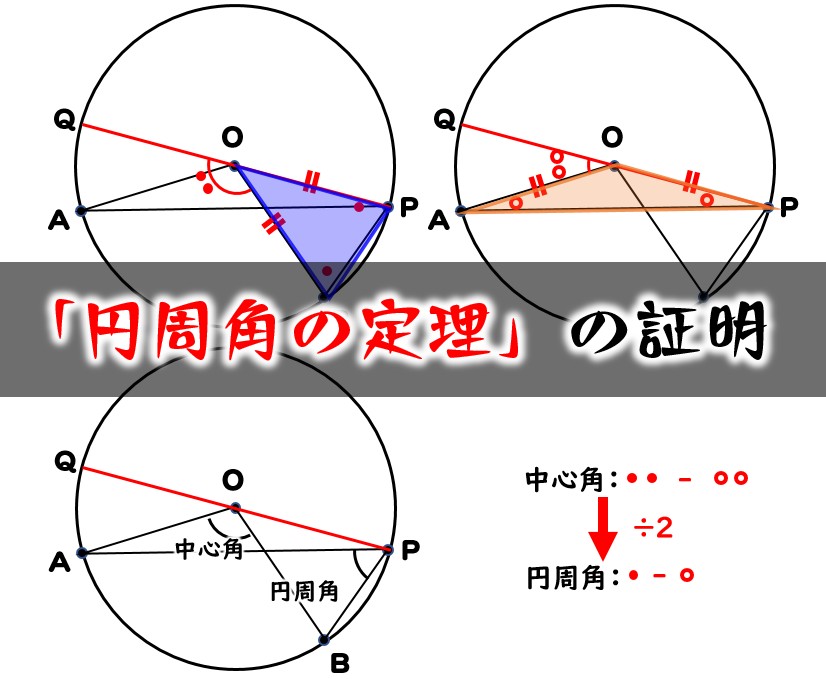



円周角の定理の証明 図で分かりやすく解説 数学fun



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
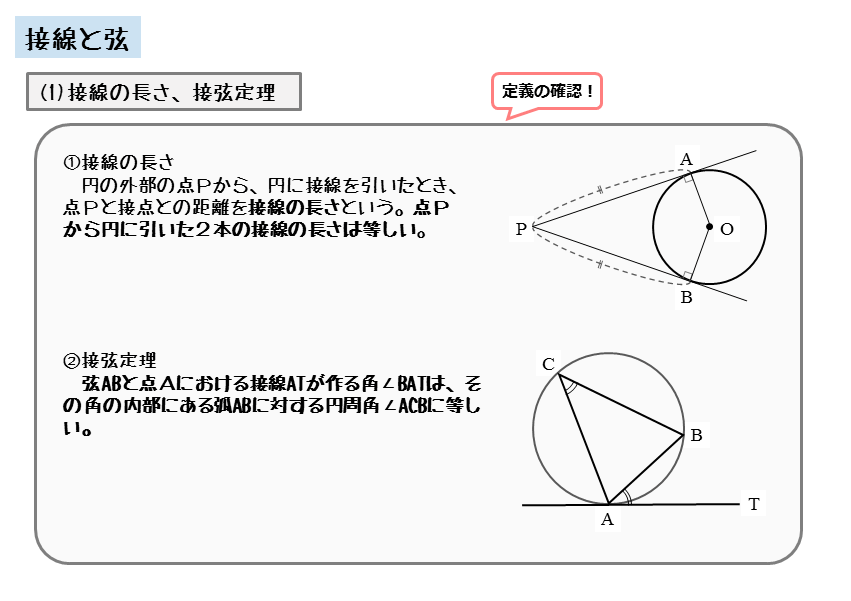



図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん



円 数学 Wikipedia




高校数学a 共円条件 4点が同一円周上にある条件 受験の月




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




公立入試問題の解説 円の性質 桃李塾のブログ



1
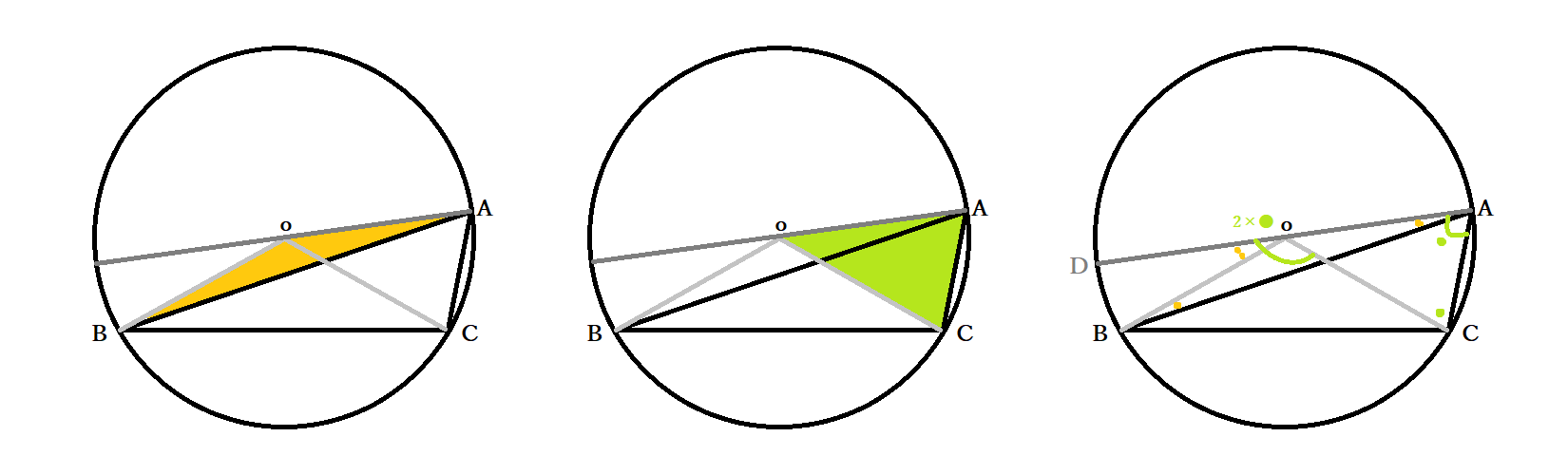



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




これ説明してくれる人いますか なんでこうなるのか分かりません Clear




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
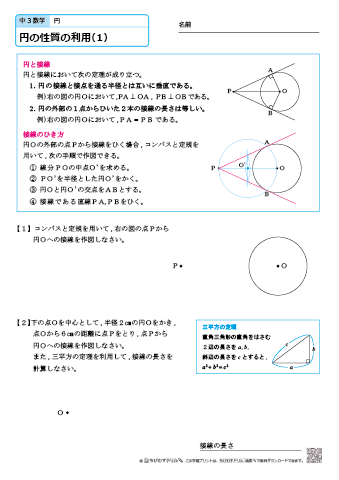



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
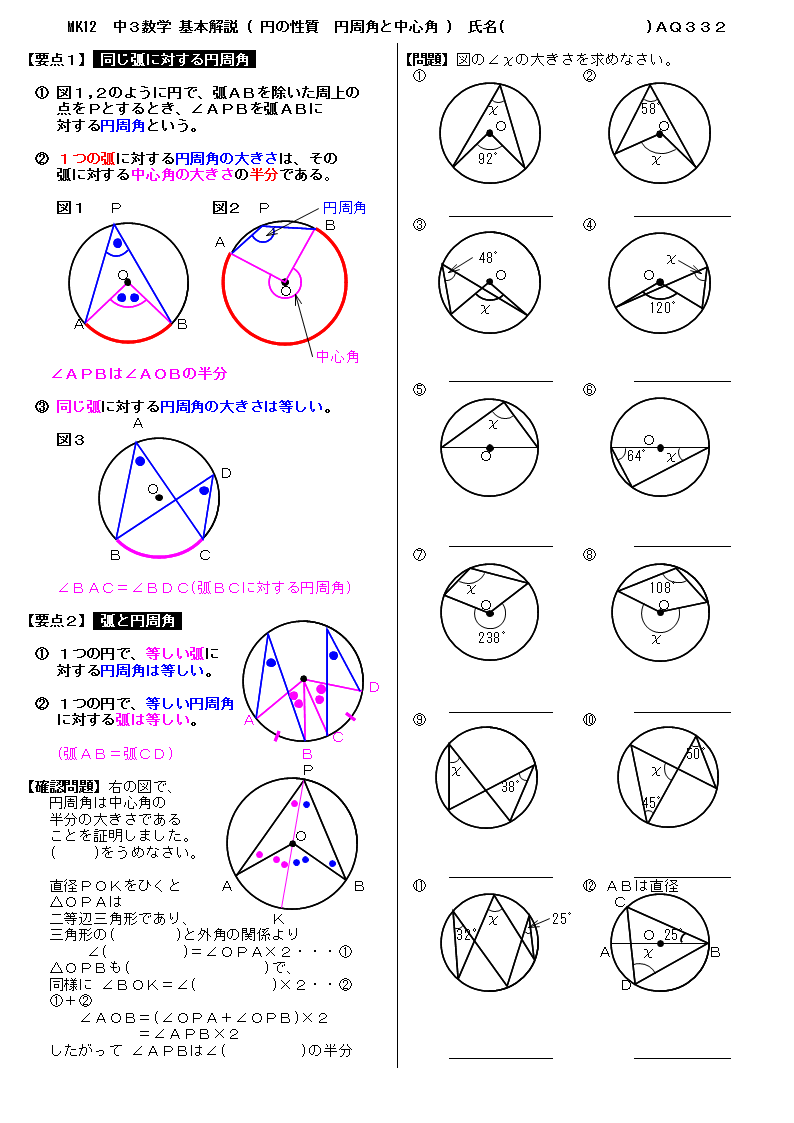



無料 中3数学 基本解説 問題プリント 332 円の性質 円周角と中心角



円周角



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
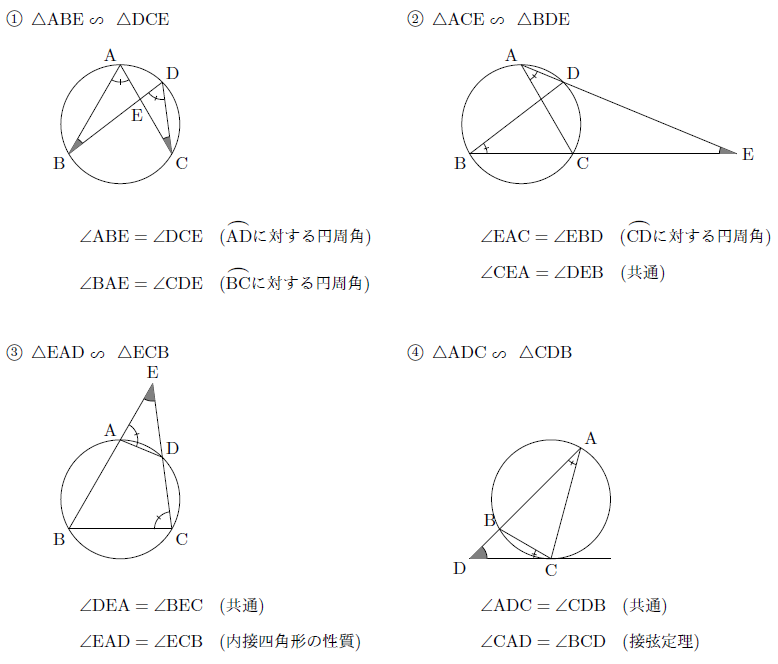



円と相似 まなびの学園
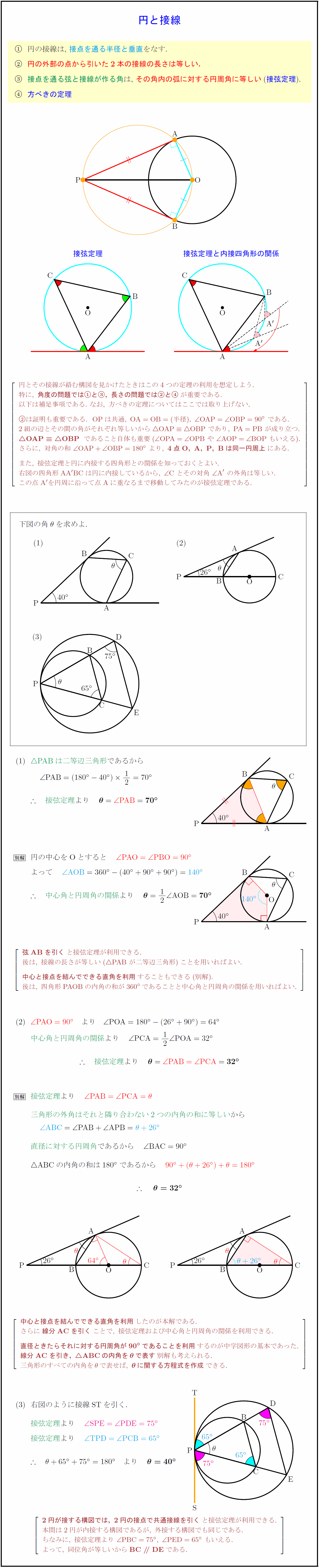



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学



円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円の性質 数学の要点まとめ 練習問題一覧




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



数学a 平面図形 円の性質 円の接線
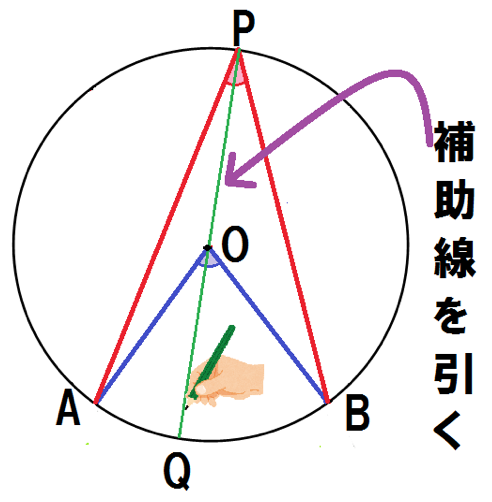



これでスッキリ 円周角の定理の証明の3つのパターン Qikeru 学びを楽しくわかりやすく




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット




中3数学 円の性質8 円周角の定理の逆 4点が同じ円周上にあることの証明 すべて無料 星組の中学数学講座




円の性質 円周角 図形 数学 高校受験講座 東京先生




中学数学 円周角の定理 円周角の定理の逆 Youtube




数学 中3 57 円周角の定理 少し応用編 Youtube




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中3 数学 円8 円の性質と証明 13分 Youtube




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



1




世界一わかりやすい数学問題集中3 6章 円の性質




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
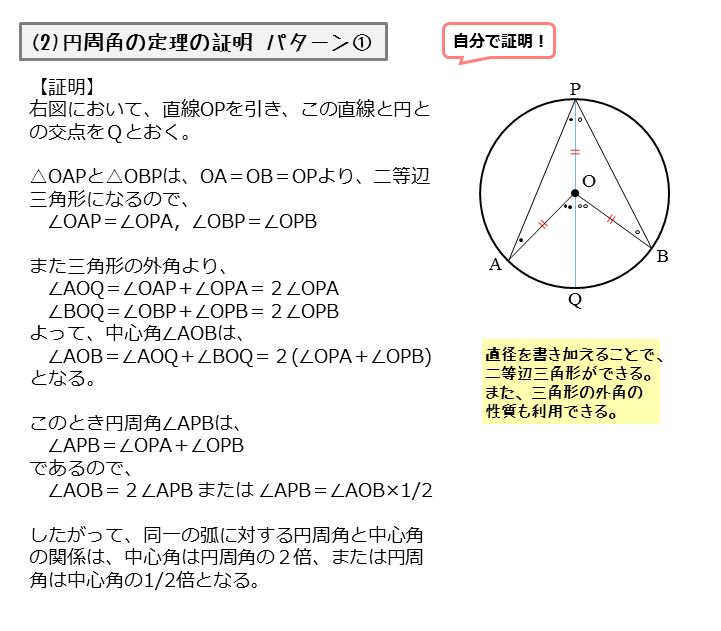



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
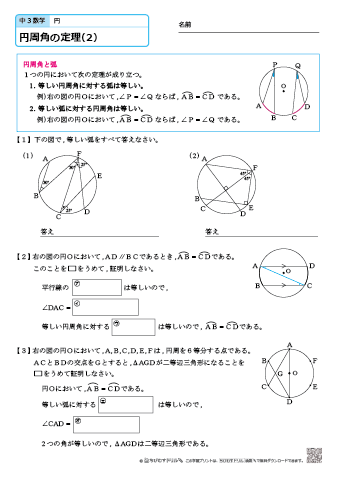



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
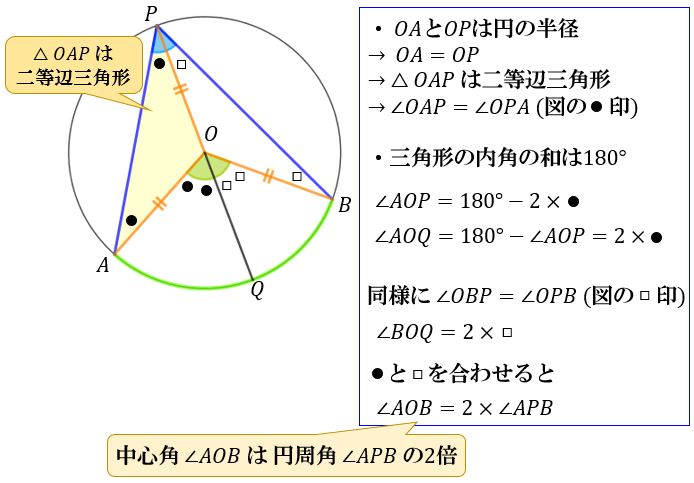



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
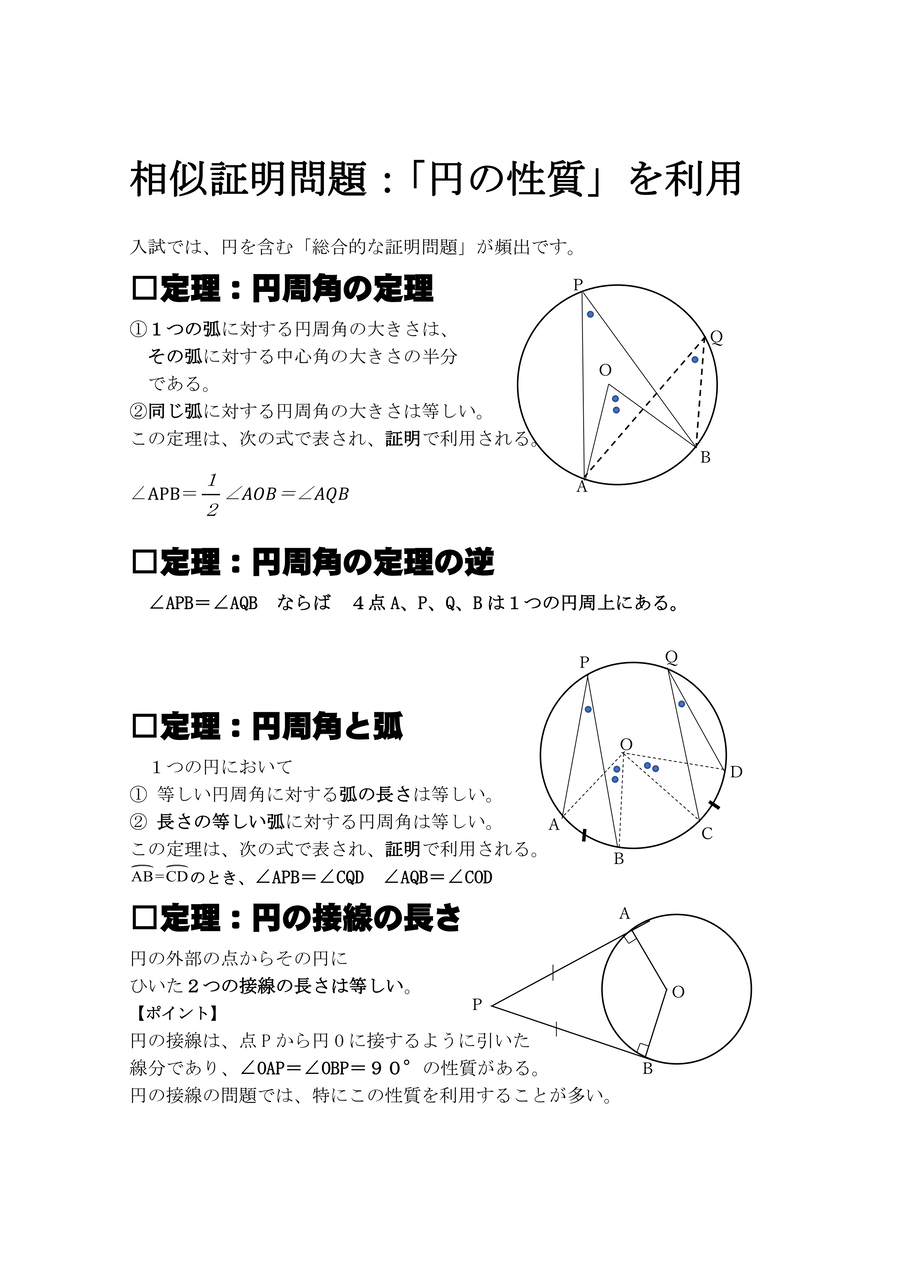



中学校数学 証明のコツ 入試問題 円



中3数学 円の性質1 円周角と中心角 証明 すべて無料 星組の中学数学講座




三角形の外接円の 4 つの性質 証明付 理数アラカルト
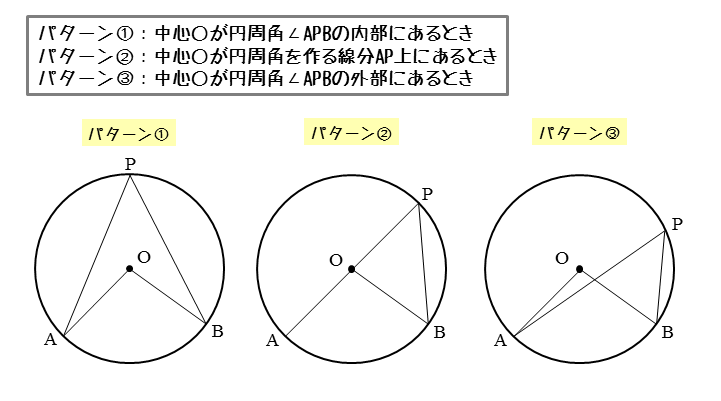



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
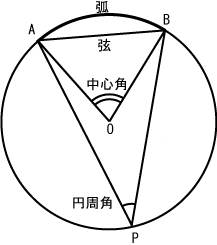



円 数学 Wikipedia




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
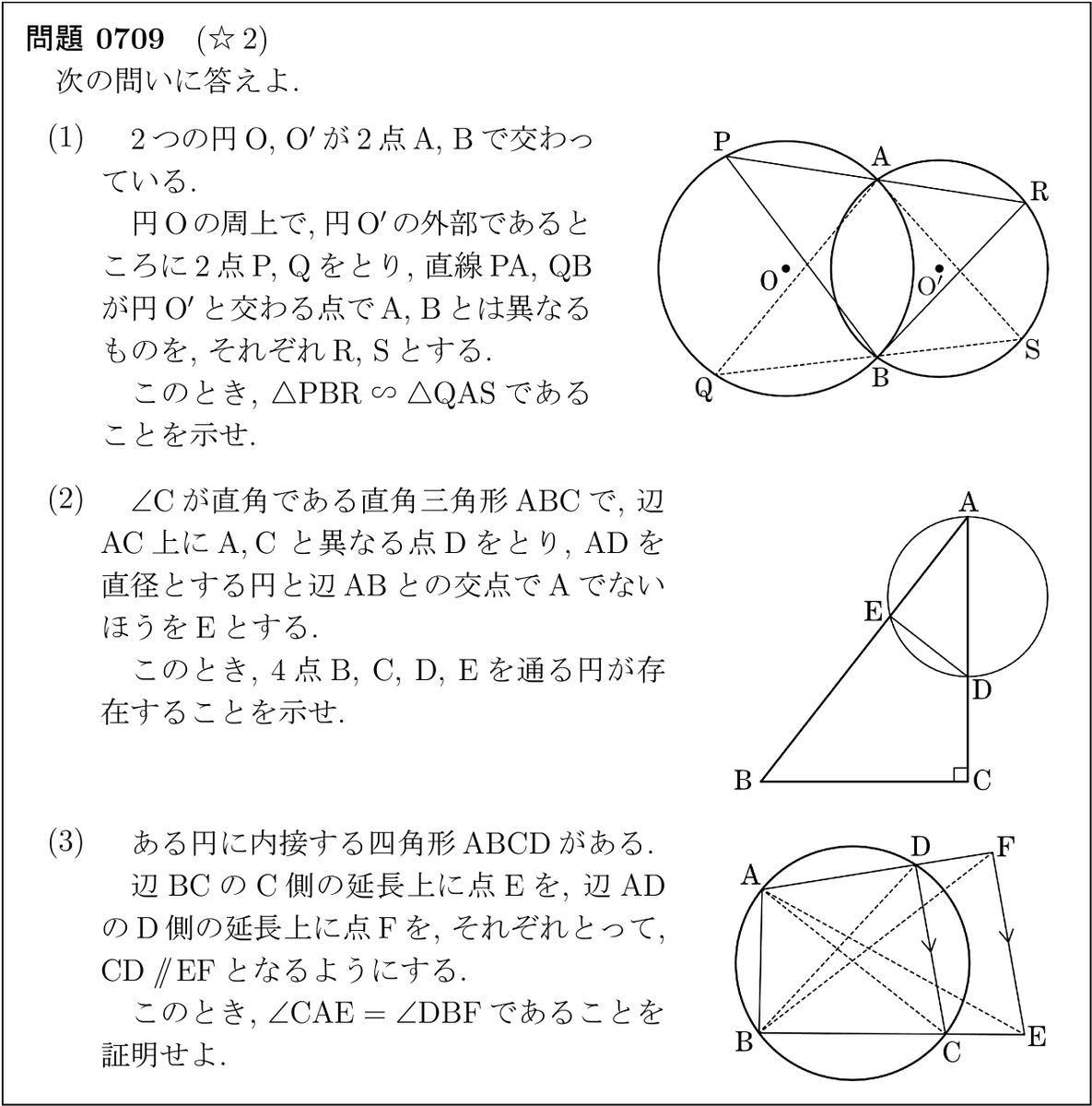



高校数学基本問題垂れ流し Ar Twitter 07 図形の性質 2 円 円周角 円に内接する四角形 4点が同一円周上にある条件と証明




中学数学 よく出る円と相似の融合問題 Pikuu




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




中3数学 円の性質18 円の性質を利用した証明 すべて無料 星組の中学数学講座
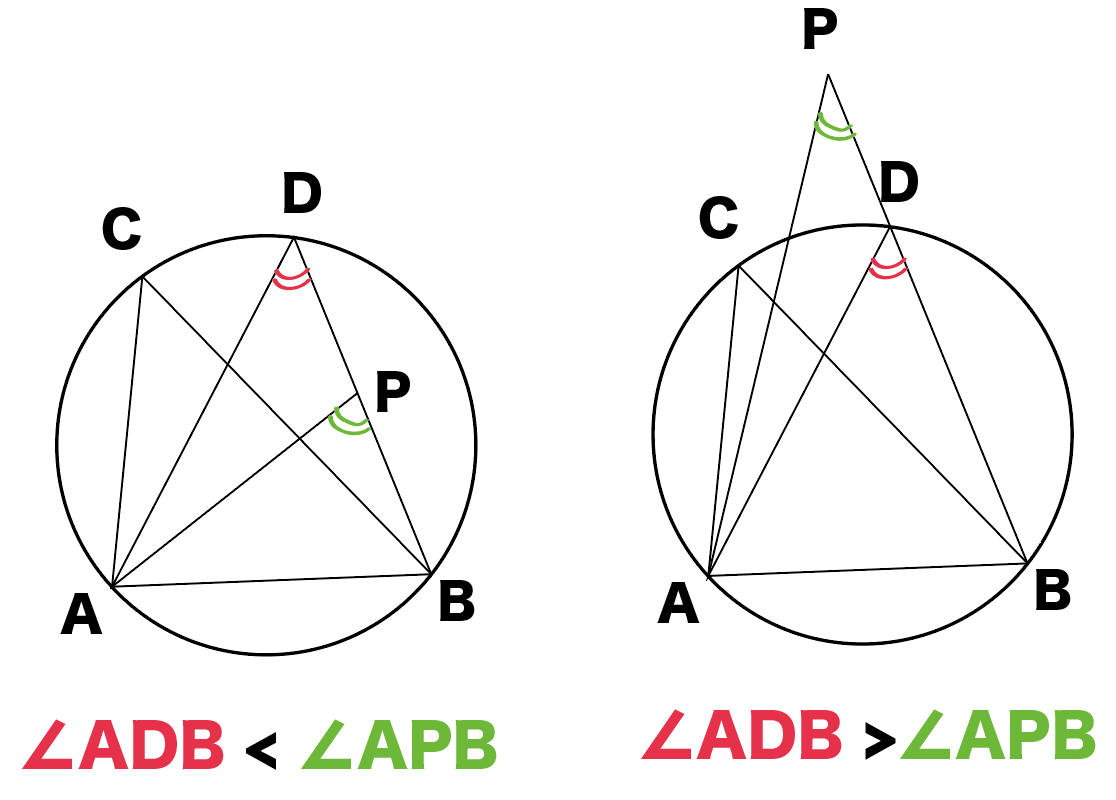



3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく



円周角の定理の逆の証明
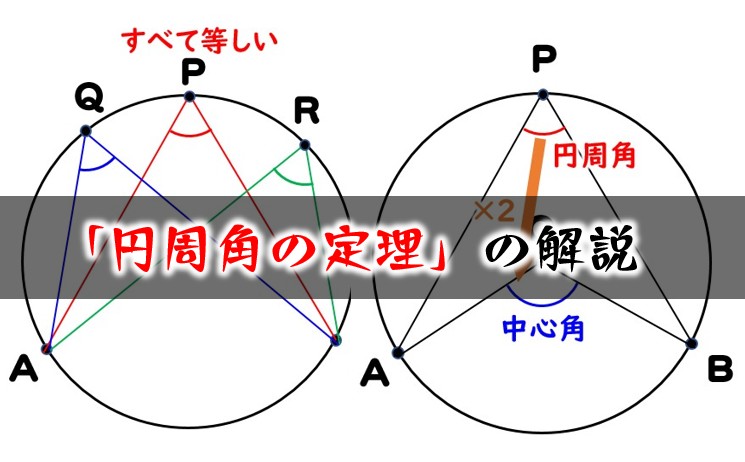



円周角の定理の解説 問題の解き方 数学fun




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



1




円の性質の利用 チーム エン
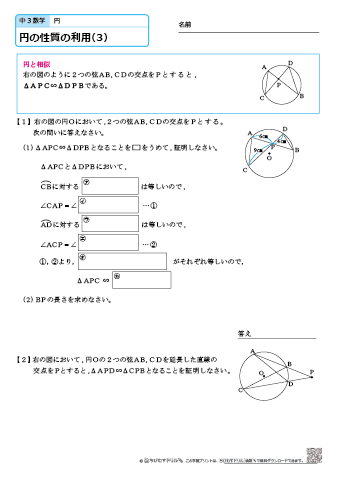



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
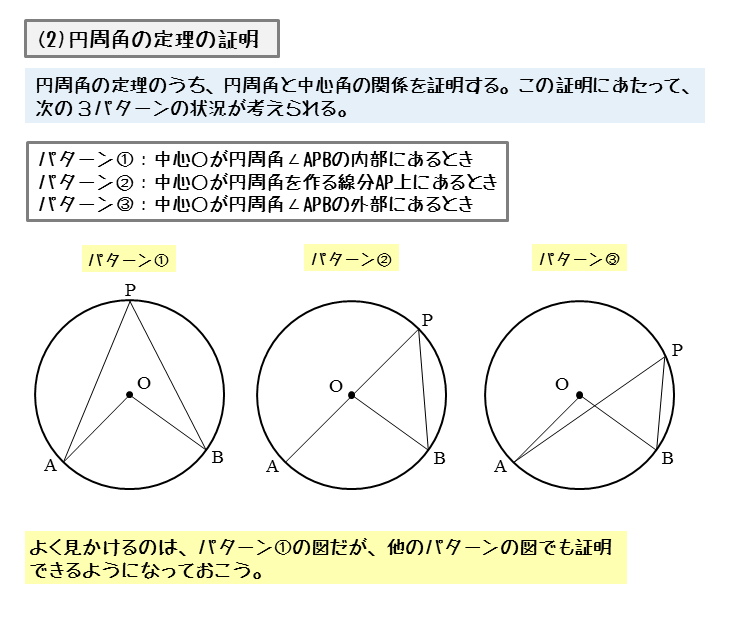



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
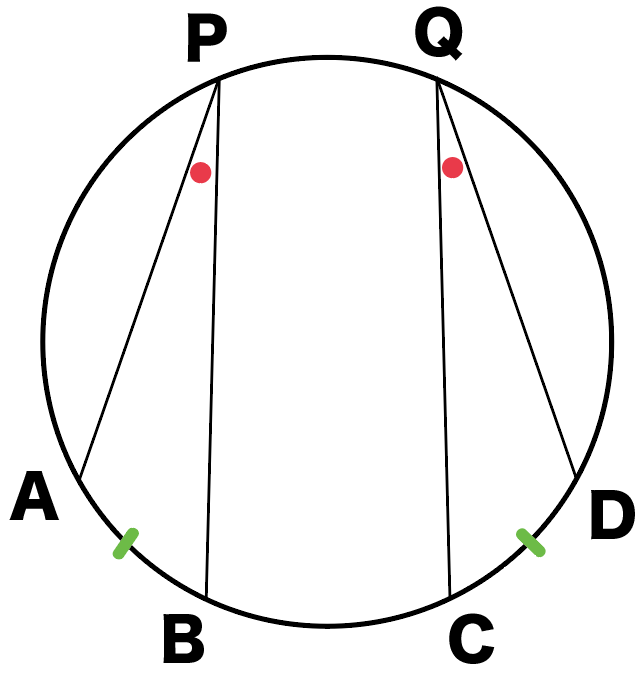



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
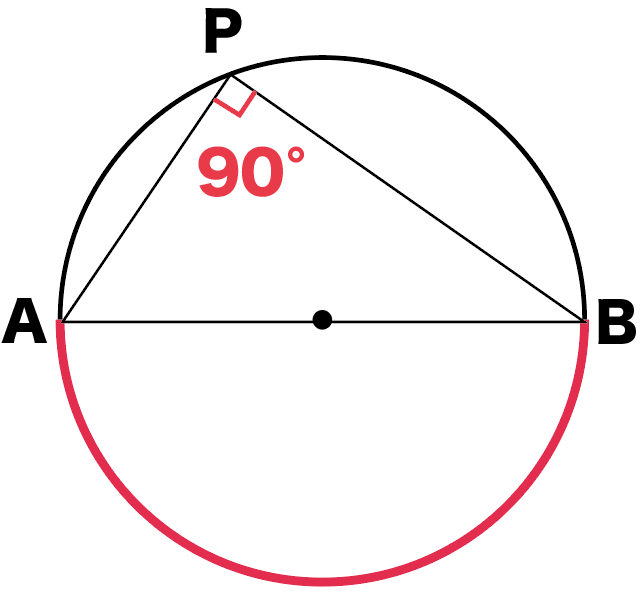



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
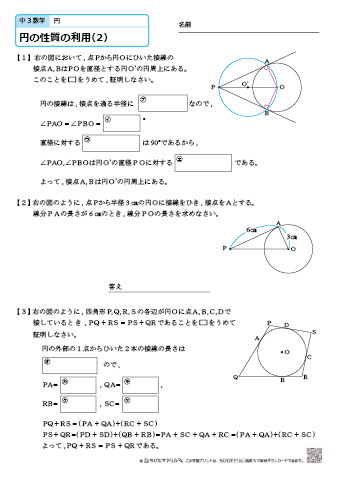



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
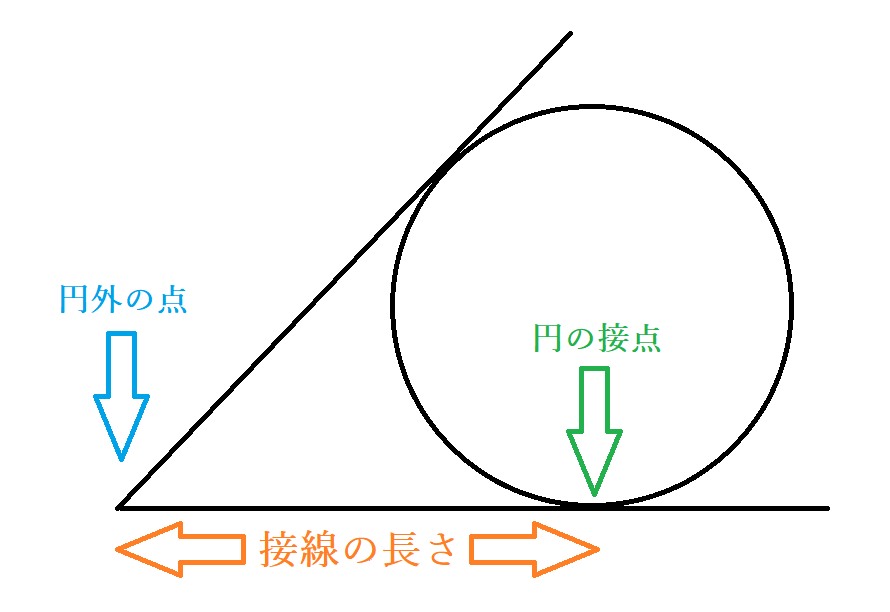



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



円周角
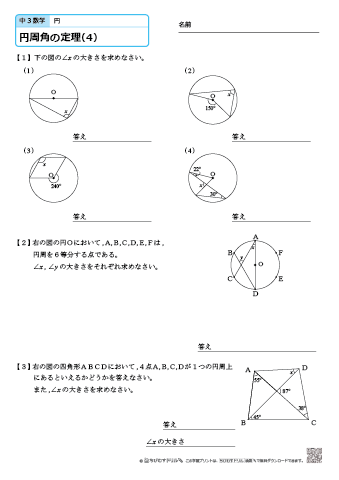



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
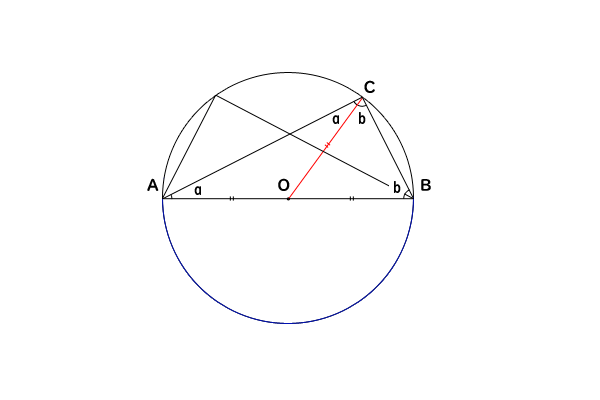



円周角の定理とその逆の証明 高校数学マスター
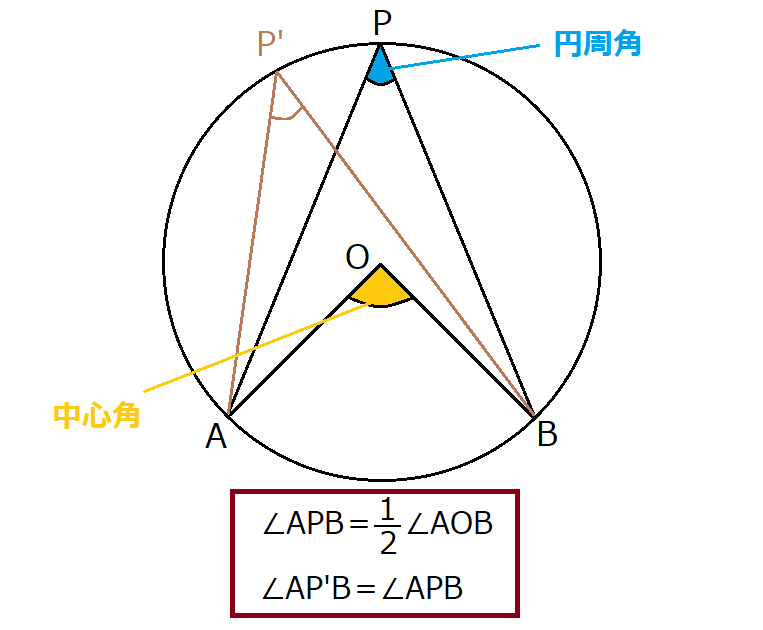



円周角の定理の証明を3つ紹介 逆も把握しよう ヒデオの情報管理部屋all Rights Reserved



0 件のコメント:
コメントを投稿